Problem Statement:
In this problem High Tech High Chula Vista wanted to put up their own flag on the flagpole in the front of the school. Our job was to try and figure out the height of the flagpole. We had to use multiple methods to try to do so.
Process & Solution:
At the very beginning of this problem we had to make a guess for what the height of the flagpole could be. We had to put a minimum height and a maximum height. My minimum height guess was 25 feet, and maximum was 35 feet. We also learned a new math word called similarity, and the easiest way to sum up similarity and what it is, would be just saying that similarity means same shape, different size. That is all it is.
Shadow Method:
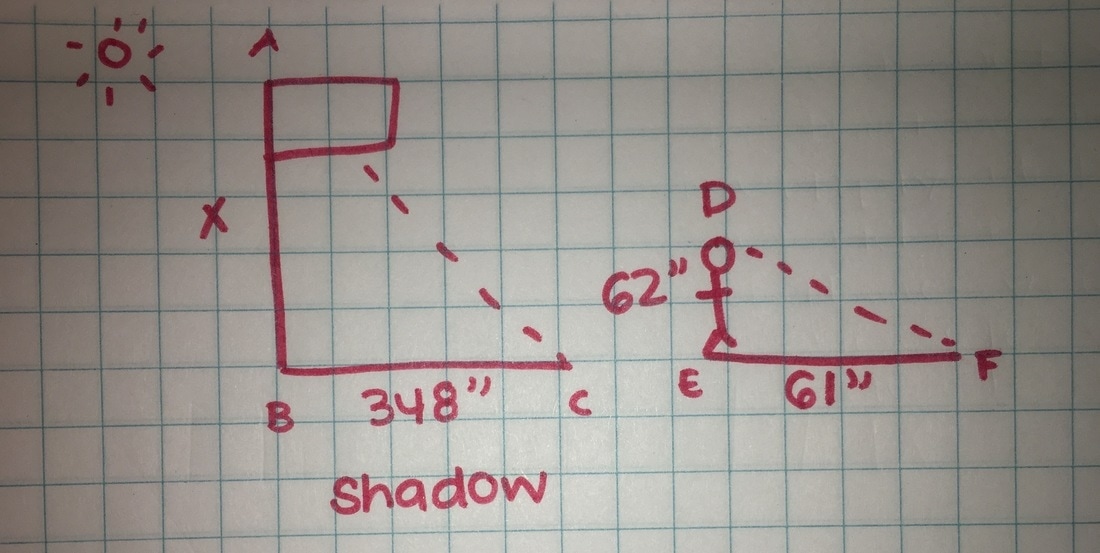
The shadow method was by far the least accurate method to use to try to solve this problem. We had to try and compare our own bodies shadow to the shadow of the flagpole. In this method, we had to use the Angle Angle Theorem or AA Theorem for short. We knew this was AA because they both had right angles. Once we had the proportions, we plugged in our table mates height and his shadow. His height was 5¨11 and his shadow was doubled so it was 7¨11. We left X as the height of the flagpole but got 40 for the shadow of it. We crossed multiplied this and it helped us to get our final answer of 25 feet.
Shadow Method:
The shadow method was by far the least accurate method to use to try to solve this problem. We had to try and compare our own bodies shadow to the shadow of the flagpole. In this method, we had to use the Angle Angle Theorem or AA Theorem for short. We knew this was AA because they both had right angles. Once we had the proportions, we plugged in our table mates height and his shadow. His height was 5¨11 and his shadow was doubled so it was 7¨11. We left X as the height of the flagpole but got 40 for the shadow of it. We crossed multiplied this and it helped us to get our final answer of 25 feet.
Example of it from my friend Dario
Mirror Method:
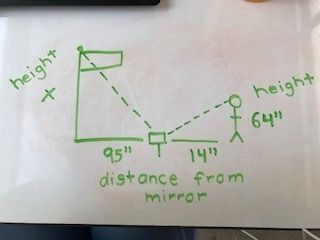
In this second method we used a mirror in front of the object and stood on the other side until we could see the object in the mirror. Once we saw the object, we measured our height and our horizontal distance from the mirror and then the distance from the mirror to the flagpole. Then we needed to also set up a proportion for this one but first we needed to prove that the triangles were similar to do so. We saw that this was using the Angle Angle Theorem because they both used two right angles and the angle where they connected was the same. Once we found our measurements, we plugged the numbers in with an X again for the flagpole. After multiplying all this we got the height of the flagpole to be 31 feet.
In this second method we used a mirror in front of the object and stood on the other side until we could see the object in the mirror. Once we saw the object, we measured our height and our horizontal distance from the mirror and then the distance from the mirror to the flagpole. Then we needed to also set up a proportion for this one but first we needed to prove that the triangles were similar to do so. We saw that this was using the Angle Angle Theorem because they both used two right angles and the angle where they connected was the same. Once we found our measurements, we plugged the numbers in with an X again for the flagpole. After multiplying all this we got the height of the flagpole to be 31 feet.
Example from my friend Dario
Clinometer:
The final method we used was a object called a Clinometer. With this, we would look through the straw and find the fourty-five degree angle with the rope. Once we found the angle, we measured our distance from the object. Once doing this, we calculated everything we measured and multiplied. From doing all of this, we got our final answer to be 31 feet.
The final method we used was a object called a Clinometer. With this, we would look through the straw and find the fourty-five degree angle with the rope. Once we found the angle, we measured our distance from the object. Once doing this, we calculated everything we measured and multiplied. From doing all of this, we got our final answer to be 31 feet.
Problem Evaluation:
This problem was a very interesting one. I never even thought of anything like it. Using angles to find out the height of a flagpole. I did not even know that could be done. I enjoyed this problem. Some parts of it were difficult but were able to be overcome.
Self Evaluation:
I feel that I did pretty good with this problem if I am being honest. Although there was obviously concepts that I struggled on and I completely bombed my test, I did understand a lot of the concepts. I was a valuable asset when it came to group work. I was able to always be there to help my group on problems when we were all struggling. As I said though, there were obviously concepts that I struggled on, but I was still able to sort of understand them. I believe for my letter grade for this whole problem I would give myself a B. I say a B because I did understood most of it and got a lot of good work done, but did struggle on some parts and completely obliterated my test.