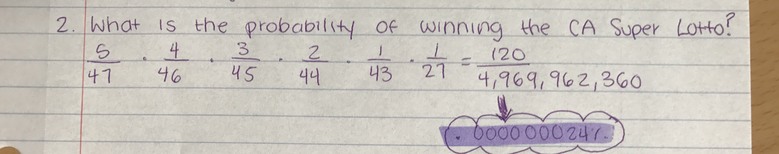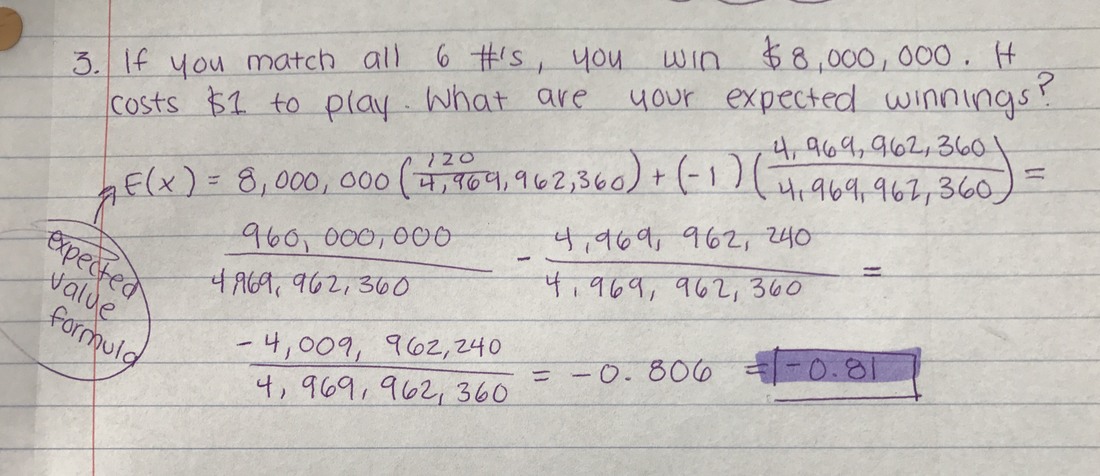*Images used are from Melissa Serrano with permission, my work was all over, so she let me use her images since we were partners.
Problem Statement
On the very first day of the semester, we jumped straight into our next unit. We began this by doing a simulation of the California Super Lotto with real money. We got a mini questionnaire type of paper. We had to fill this out with our thoughts. After this, we got into the actual simulation. We were using real money in this. You could choose to play, and if you get the winning numbers, you won $20. If you chose not to play, you got 2 free extra credit points. More than half of the class chose to not play. We had to put down 5 numbers. The only numbers we could choose from was 1-47. We also had to choose a mega number. For our mega number, we were only able to choose numbers 1-27. Everyone put there numbers down, even the ones not playing. In total in my class, only 3 people decided to give up the free extra credit and play. They all lost. After this, we continued learning about probability to figure out our final problem.
Process & Solution
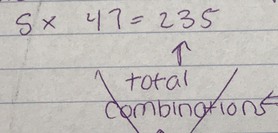
At the end of this, we had three final problems. These problems were:
- How many different number combinations are possible for a CA Super Lotto Ticket?
- What is the probability of winning the CA Super Lotto?
- If you match all 6 numbers, you win $8,000,000. It costs $1 to play. What are your expected winnings?
Let us start with the first question:
How many different number combinations are possible for the CA Super Lotto Ticket?
I began this problem in a simple way that I thought was correct. You can only choose 5 numbers (Excluding the mega number here) from 1-47. So, I just decided to multiply 5 x 47. My answer for this was 235. I saw it as correct. I then saw two classmates that had a much higher number. I was wondering how that got it and if it was even correct. I later found out that their answer was correct, and mine was way off. I decided to use their method. They used 5 as a sample space, so I did the same. I then multiplied 5 by 47, 46, 45, 44, and 43. After multiplying all of these, I got 184,072,360. After getting that, we still needed the mega number, soI multiplied that by 27 which was the sample space of the mega number. The number for that was 4,969,962,360.
- How many different number combinations are possible for a CA Super Lotto Ticket?
- What is the probability of winning the CA Super Lotto?
- If you match all 6 numbers, you win $8,000,000. It costs $1 to play. What are your expected winnings?
Let us start with the first question:
How many different number combinations are possible for the CA Super Lotto Ticket?
I began this problem in a simple way that I thought was correct. You can only choose 5 numbers (Excluding the mega number here) from 1-47. So, I just decided to multiply 5 x 47. My answer for this was 235. I saw it as correct. I then saw two classmates that had a much higher number. I was wondering how that got it and if it was even correct. I later found out that their answer was correct, and mine was way off. I decided to use their method. They used 5 as a sample space, so I did the same. I then multiplied 5 by 47, 46, 45, 44, and 43. After multiplying all of these, I got 184,072,360. After getting that, we still needed the mega number, soI multiplied that by 27 which was the sample space of the mega number. The number for that was 4,969,962,360.
What is the probability of winning the CA Super Lotto?
This problem was more simple, I just multiplied everything in the picture below. For the numerator, I got 120, and the denominator was 4,969,962,360. That wasn't the probability though. I had to find the percentage of what it would be. To find this was very simple. All I had to do, and this is something we have been doing throughout our whole time learning probability, was divide 120 by 4,969,962,360. By doing that, it would have us a decimal number, and that would be the percentage and probability. So I did that and got .000000024%.
This problem was more simple, I just multiplied everything in the picture below. For the numerator, I got 120, and the denominator was 4,969,962,360. That wasn't the probability though. I had to find the percentage of what it would be. To find this was very simple. All I had to do, and this is something we have been doing throughout our whole time learning probability, was divide 120 by 4,969,962,360. By doing that, it would have us a decimal number, and that would be the percentage and probability. So I did that and got .000000024%.
If you match all 6 numbers, you win $8,000,000. It costs $1 to play. What are your expected winnings?
For this last problem, we had to use the final formula that we learned. It was the Expected Value formula as taught in class. It looked like this: E(X)=∑XiPi. To start, I plugged in 8,000,000 for X because if you match all 6 numbers, that is how much you win. Then I had to plug in 120 over 4,969,962,360 for i which is the probability of winning and multiply it. After that, added -1 and multiplied that by the other i which came out to be 4,969,962,360 over 4,969,962,360.
After this, I multiplied 8,000,000 by 120 and got 960,000,000. I then put 960,000,000 and 4,969,962,360. After this, I multiplied -1 by 4,969,962,360 and got -4,969,962,340 over 4,969,962,360. After, you subtract that and get -4,009,962,240 over 4,969,962,360. You then divide this and find that your expected winnings will be -0.81.
For this last problem, we had to use the final formula that we learned. It was the Expected Value formula as taught in class. It looked like this: E(X)=∑XiPi. To start, I plugged in 8,000,000 for X because if you match all 6 numbers, that is how much you win. Then I had to plug in 120 over 4,969,962,360 for i which is the probability of winning and multiply it. After that, added -1 and multiplied that by the other i which came out to be 4,969,962,360 over 4,969,962,360.
After this, I multiplied 8,000,000 by 120 and got 960,000,000. I then put 960,000,000 and 4,969,962,360. After this, I multiplied -1 by 4,969,962,360 and got -4,969,962,340 over 4,969,962,360. After, you subtract that and get -4,009,962,240 over 4,969,962,360. You then divide this and find that your expected winnings will be -0.81.
Problem Evaluation
This problem has been one of the most fun problems for me. I have really been able to easily understand it and always know what we are doing, and what we need to solve. I never was lost. It kind of sucks that it ended so early. I was having so much fun doing it. This was a problem that I was actually able to understand right away and not need to ask to many questions on. It wasn't frustrating or anything. I was able to do everything on time with no problems.
Self Evaluation
If I were to give myself a grade on this, it would be an honest A. Out of all the other problems we have done before. This has been the most well understood to me. I was able to do most of these problems on my own with no help. There was only a couple areas where I needed help, but after the help, I was able to understand everything clearly. I also was able to help others with this. This was honestly very good for me.
Peer Edits:
- Add clearer images (added Melissa's images)
-Be more descriptive
- Add more images
- Bold numbers
- Add clearer images (added Melissa's images)
-Be more descriptive
- Add more images
- Bold numbers