Problem Statement
In this problem that we called the "Fireworks Problem" we were given a certain problem. This is what the problem was about and looked like.

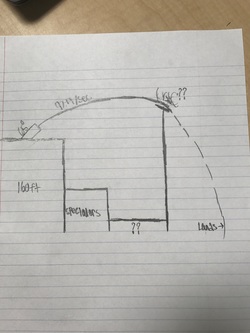
As you can see, we are trying to help to figure out what they are asking. We were given a couple of known factors in the problem to help us better understand and figure the problem out. On the left side you can see the givens. From those, we were supposed to find the unknowns as also seen.
Process & Solution
We orignally started this problem with some certain questions that we needed answered in order to help us more to understand and solve the problem. These are some examples of the questions:
- What is the height of the tower?
- How many fireworks are there?
- What is the distance from the launch to the spectators?
- What degree will the fireworks be launched from?
- Etc.
From answering these questions, we were able to draw an image of what we were given, and of what we need in order to further move on with this problem.
- What is the height of the tower?
- How many fireworks are there?
- What is the distance from the launch to the spectators?
- What degree will the fireworks be launched from?
- Etc.
From answering these questions, we were able to draw an image of what we were given, and of what we need in order to further move on with this problem.
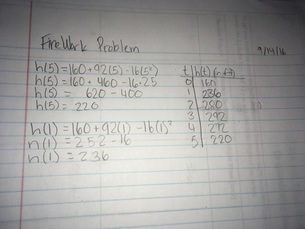
After this, we created an X-Y table to help us to find the vertex of the fireworks. The vertex is the maxium height that the fireworks would reach. From this we were able to find that the maxium height would be at 3 seconds. We then went deeper into it, and found that 2.5 seconds would actually be the highest, even higher than 3 seconds. So, they vertex of the fireworks would have to be somewhere between 2 and three, but then again. Isn't there infinite number practically in between 2 and 3? Well that is where we got a bit confused on where the actual height could be.
*Credit to Aaron for the image
We decided to take a little break from that problem so we could find concepts to help us better find the answers we needed. So, we jumped straight into the world of quadratics. We started learning about this process by learning how to multiply binomials. We then learned how to factor intercepts. Putting these two together helped us to solve for special points on a parabola. We saw what the standard form had in common with the intercepts in the equations. We saw the constant of the equation was the same as the Y-Intercepts on the parabola. In factored form you were able to see that the X-Intercepts were also there. We then learned about vertex form. With vertex form, we were able to find the Y-Intercepts, X-Intercepts, and the Vertex of the parabola.
After this, we learned about the actual quadratic formula. This is exactly what we needed to solve the fireworks problem. It was sort of the last step we needed for it. Once we learned this and mastered it, we went back to the fireworks problem. We looked back at the two orginal equations. These equations were h(t)=160+92t-16t^2 and d(t)=92t/tan65. h(t)=160+92t-16t^2 would give us the max height or vertex of the fireworks. d(t)=92t/tan65 would give us the distance that the fireworks would travel. There was still something missing though. The time. In order to find the time, we needed to plug in the first equation into the quadratic formula.
When the equation was plugged in, we were able to find the time for everything. We discovered that the time the fireworks would reach their max height was at 2.88 seconds. The time that they would then land would have been at 7.15 seconds.
After we found that, we plugged both of them into the equations for t. We saw that 2.88 seconds will reach a max height of 292.32 feet. At 7.15 seconds, the fireworks would reach the ground going as far as 306.69 feet. After finding those, the fireworks problem was finally over. We solved for everything and finally figured everything out.
Problem Evalution
To be completely honest. I actually liked this problem a little. I started it thinking that I was not going to like it at all because I usually never like these types of problems. Once my group and I started getting more into it, it started to get easier and more understandable. I was able to solve some of the things and help my group much easier than before on these problems. I actually thought this problem was simpler than other problems that we have done in the past. I also think that during this problem, my group pushed me to do more in it and really understand it. I was able to learn some things and grow stronger in certain areas while working on this problem with my group. For example, I was able to really push myself to think more during this. Overall, this problem was not too bad, and I had a good time doing it with my group.
Self Evalution
Our whole quadratics unit was about 12 weeks. This unit started for me pretty easy. As we got more into it, it still wasn't so bad, I was able to do the work on my own and not really need help with much. A bit later, I started to struggle with it more. I tended to need to ask more questions to people, and ask for a lot more help. Towards the end I started to understand things better, but not completely. For example, on the quadratic formula